Exploiting a 40 year-old design choice to speed up vector search

A while ago, I came across a post on reddit about a user’s experience speeding up the rav1d video decoder by 1%, which inspired me to try a similar trick to speed up sorting f32’s in my vector database.

The hack from the post involved swapping field-wise equality for byte-wise equality, which translated into a custom impl of PartialEq for the struct in question. Doing this greatly reduced the number of instructions in the resulting assembly code by almost half and yielded tangible speedups in the decoder.

So instead of this :

use zerocopy::{AsBytes}

#[derive(PartialEq, AsBytes)]
#[repr(C)]
pub struct Foo{
  a: i32,
  b: i32
}

You’d write :

use zerocopy::{AsBytes}

#[derive(AsBytes)]
#[repr(C)]
pub struct Foo{
  a: i32,
  b: i32
}

impl PartialEq for Foo{
  fn eq(&self, other: &Self) -> bool {
    // NOTE: `as_bytes` comes from #[derive(AsBytes)]
    self.as_bytes()  == other.as_bytes()
  }
}

Now when we consider the equality of two &Foo’s we just look at &[u8] slices instead of doing a field-by-field check.

In vector search applications, a non-negligeable amount of time is spent ordering f32’s to determine if an item is a nearest neighbour or not. I figured it was the perfect setting to try out the approach above.

Rust, f32, Ord, and sadness

In rust, f32 doesn’t implement Ord or Eq. Consulting the docs on NaN’s explains why :

• It is not equal to any float, including itself! This is the reason f32 doesn’t implement the Eq trait.
• It is also neither smaller nor greater than any float, making it impossible to sort by the default comparison operation, which is the reason f32 doesn’t implement the Ord trait. [link]

This is why you need a crate like ordered-float if you wish to work with containers like std::collections::BinaryHeap<T> that enforces the T: Ord trait bound to perform sorting internally.

ordered-float is great most of the time, but in the context of vector search I think it’s a bit overkill.

For starters, we’re only working with non-negative f32’s coming from distance metrics, not the whole representable range. For another, the ordered-float crate also implements Hash for it’s OrderedFloat<f32> wrapper type which adds some lines of code to the final executable that we don’t really need.

On top of this, the project itself is around ~3k SLOC, while a bare-bones implementation doing only what we need takes less than 50 SLOC.

Getting sneaky with IEEE 754

Floats are generally made up of 3 components: a sign bit; some exponent bits; and some mantissa (fraction) bits. This format goes all the way back to the IEEE 754 Standard from 1985, and is what’s going to help us here today.

By playing around with the number of bits you allocate between the exponent and mantissa you can cover a wider dynamic range or achieve higher precision depending on your use-case. bf16 for instance allocates fewer fraction bits while maintaining the same number of exponent bits as f32, making it less precise but covering the same dynamic range.

To convert from a 32-bit integer back to an f32 you use the following formula: $$ x = (-1)^{\text{sign}}\times2^{(\text{exponent}-127)}\times\left(1+\sum_{i=1}^{23}b^{(fraction)}_{i}2^{-i} \right) $$

While it may be true that $-x\leq x$ in f32-world, the same relationship doesn’t hold when we interpret those same f32’s as u32’s. It’s enough to look at the sign bit and see why; any negative number has the most significant bit set to 1 which automatically makes it larger as an integer than its positive counterpart.

This is why statements like (f32::MAX).to_bits() < (-0.0f32).to_bits() evaluate to true.

Ok, so we can’t just compare &[u8]’s and call it a day… or can we ?

Recall that all the f32’s we need to sort come from distance calculations (e.g. cosine, euclidean, hamming, etc.) so we can guarantee that they’re always $\geq 0$ ! This means it’s totally valid to compare the f32’s as if they were integers.

The only edge case we really need to look out for is a -0.0f32 showing up from float arithmetic, but we can add an assert to filter cases like these out.

Ordering your own floats

I’ll be honest, the code I’m about to share is pretty underwhelming, it’s exactly what you’d expect if you’ve been reading along so far. But hey, it works !

Here it is :

#[derive(Default, Debug, Clone, Copy)]
pub struct OrderedFloat(pub f32);

impl PartialEq for OrderedFloat {
    fn eq(&self, other: &Self) -> bool {
        self.0.to_bits().eq(&other.0.to_bits())
    }
}

impl Eq for OrderedFloat {}

impl PartialOrd for OrderedFloat {
    fn partial_cmp(&self, other: &Self) -> Option<std::cmp::Ordering> {
        Some(self.cmp(other))
    }
}

impl Ord for OrderedFloat {
    fn cmp(&self, other: &Self) -> std::cmp::Ordering {
        self.0.to_bits().cmp(&other.0.to_bits())
    }
}

This struct does everything we need; no more, no less !

Note that we should add some kind of check in the constructor to ensure our OrderedFloat isn’t being built with a negative number, but for the sake of this blog post I’ll skip that.

Benchmark

Recall that way back at the start of this post I stated the goal was to see if comparing f32’s byte-wise was faster doing “proper”f32 comparisons. Well let’s do that.

We’ll benchmark how long it takes to build a BinaryHeap from both my OrderedFloat and the ordered_float::OrderedFloat::<f32>.

As an aside, I recently switched from criterion to divan for benchmarking due to it’s simple and expressive syntax, and I’ve gotta say I’ve been loving it ! 🎉

use std::collections::BinaryHeap;

use divan::{self, Bencher, counter::BytesCount};
use f32_blogpost_bench::OrderedFloat;
use rand::Rng;

fn main() {
    divan::main();
}

#[divan::bench(consts = [10, 100, 1000, 10000])]
fn custom_ord_impl<const N: usize>(bencher: Bencher) {
    bencher
        .with_inputs(|| {
            let mut nums = [f32::default(); N];
            rand::rng().fill(&mut nums);
            let nums_cmp: Result<Vec<_>, &'static str> =
                nums.into_iter().map(OrderedFloat::try_from).collect();

            nums_cmp.unwrap()
        })
        .bench_values(|vec| BinaryHeap::from(vec));
}

#[divan::bench(consts = [10, 100, 1000, 10000])]
fn ordered_float_crate<const N: usize>(bencher: Bencher) {
    bencher
        .with_inputs(|| {
            let mut nums = [f32::default(); N];
            rand::rng().fill(&mut nums);
            let nums_cmp: Vec<_> = nums
                .into_iter()
                .map(ordered_float::OrderedFloat::<f32>)
                .collect();

            nums_cmp
        })
        .bench_values(|vec| BinaryHeap::from(vec));
}

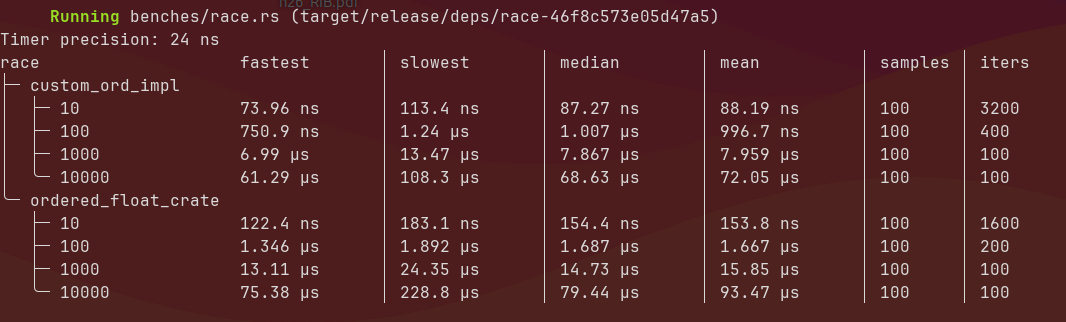
As you can see, by comparing f32s via their &[u8] representation we’re able to fill a BinaryHeap twice as quickly on average!

Conclusion

I’ll be the first to admit that these speedups are relatively small when you consider that a typical search usually takes O(10ms), but I find it intellectually satisfying that we were able to leverage the structure of our data to squeeze out some speed gains.

To summarize everything, in this article we exploited both the fact that f32’s coming from distance calculations are never negative, as well the 32-bit layout of a single-precision float, in order to compare f32’s more efficiently.

There’s still much work to be done to speed up the vector db further, but we take speedups where we can get them :)