TLDR: I used a spike-and-slab prior instead of the unit gaussian to model the latent distribution of a variational autoencoder.

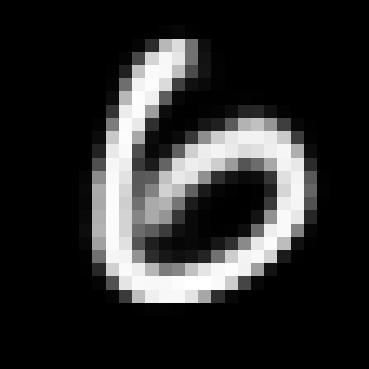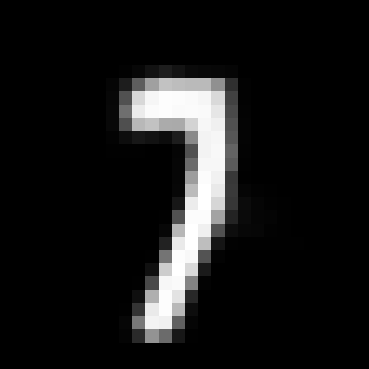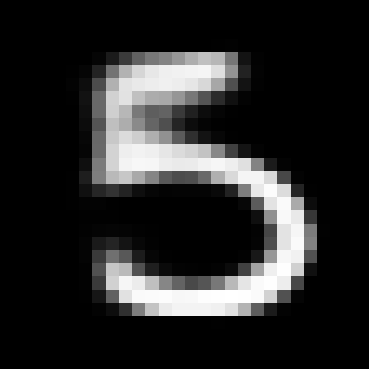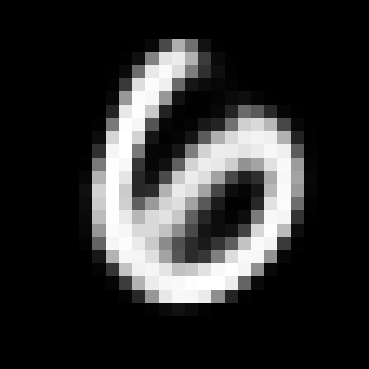
Theory

Before diving into it, I thought I’d mention that I’ve included a quick refresher on the math behind VAEs at the end of this article ifyou’re feeling rusty ;)

The main idea is to assume a prior on the latent space where each latent, $z_{i}$, of the encoded sample, $x$, has some probability, $p$ of being turned “on” or “off”. For $c\in \mathbb{R}$, $|c|<1$ we have for each dimension

$$\begin{align*} z_{i} | \gamma_{i} &\sim (1-\gamma_{i})\cdot \mathcal{N}(0, c^{2}) + \gamma_{i}\cdot \mathcal{N}(0, 1)\\ \gamma_{1}, \gamma_{2}, ..., \gamma_{d}|p &\overset{iid}{\sim} Be(p) \end{align*}$$

Our goal is to have a VAE that learns how to encode and decode samples in a sparse fashion. Sparse representations - or ones where a lot of information can be “zeroed out” - are nice mathematically and in a sec we’ll see what that looks like with the MNIST dataset. Note that we can throttle the sparsity through our choice of $p$, where $p$ close to one means most of the embedding dimensions are uninformative.

We’ll also assume $z_{i}|x \sim \mathcal{N}(\mu_{\phi}(x), \sigma^{2}_{\phi}(x))$ and that $x_{i}|z \sim Be(\theta(z))$. That last choice is mainly since I’m going to show some examples using grayscale images and we want our generated outputs being a value truncated between 0 and 1.

Okay so here’s the bad news: unfortunately no closed form for the KL-divergence between our mixture model prior and the posterior exists. The good news: we can just estimate the KL loss through Monte Carlo pretty easily:

$$\begin{align*} D_{KL}(q_{\phi}(z|x)||p(z)) &= \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log \frac{q_{\phi}(z|x)}{p(z)}\right] \\ &\approx \frac{1}{N}\sum_{i=1}^{N} \log q_{\phi}(z^{(i)}|x) - \log p(z^{(i)}), \quad z^{(i)}\sim q_{\phi}(\cdot | x)\\ \end{align*}$$

One last thing, since we’re considering a Bernoulli framework for our probibalistic decoder, the first term in the ELBO breaks down to binary cross entropy (BCE) loss if we assume conditional independence. Indeed,

$$\begin{align*} \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log p_{\theta}(x|z)\right] & = \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log \prod_{i}p_{\theta}(x_{i}|z)\right]\\ &\approx \sum_{i} \log \left( \theta_{i}(z))^{x_{i}}(1-\theta_{i}(z))^{(1-x_{i})}\right), \quad z \sim \mathcal{N}_{d}(\mu_{\phi}(x), \Sigma_{\phi}(x))\\ & = \sum_{i} x_{i}\cdot \log(\theta_{i}(z)) + (1-x_{i})\cdot \log(1-\theta_{i}(z))\\ \end{align*}$$

So we’re looking to minimize the binary cross entropy pixel-wise across the image.

Code

Using PyTorch and torch.distributions we can easily implement everything we were just talking about.

First let’s handle the distributional aspects:

from torch import nn 
import torch.distributions as dist 
import numpy as np 

class SpikeAndSlab():
    def __init__(self, spike, slab, p):
        assert(0<=p and p<=1)
        
        self.spike = spike
        self.slab = slab
        self.p = p
    
    def sample(self, k=1):
        sample_ = lambda : self.spike.sample((1,)) if np.random.uniform(0,1)<self.p else self.slab.sample((1,))
        samples = [sample_() for i in range(k)]
        return torch.cat(samples)
    
    def log_prob(self, samples):
        # logsumexp :)
        spike_logit = torch.log(torch.tensor(self.p)) + self.spike.log_prob(samples)
        slab_logit = torch.log(torch.tensor(1-self.p)) + self.slab.log_prob(samples)
        
        return torch.logsumexp(torch.cat((spike_logit.unsqueeze(1), slab_logit.unsqueeze(1)),1),1)

def kl_divergence(q, p, k=10):
    # k sample monte carlo estimate for kl-divergence 
    samples = q.sample((k,))
    return torch.mean(q.log_prob(samples) - p.log_prob(samples))

Now for the loss terms:

mu, log_var = vae_model.encoder(x)

z = mu + torch.exp(0.5*log_var)*torch.zeros_like(mu).normal_()
decoded = vae_model.decoder(z)

#reconstruction loss
recon = nn.functional.binary_cross_entropy(decoded, data, reduction='sum')

#kl divergence
pz_x = dist.normal.Normal(mu, torch.exp(0.5*log_var))

p = 0.8 
spike = dist.normal.Normal(0,np.sqrt(0.05)) 
slab = dist.normal.Normal(0,1)
pz = SpikeAndSlab(spike, slab, p)

kl = kl_divergence(pz_x, pz,k=10) 

#total loss
loss = recon + kl 

I’ve left out the architectures for the encoder and decoder but since the MNIST dataset is fairly simple most choices will do. Notice also that we made use of the LogSumExp trick to handle computing the log probabilities under the spike and slab prior.

With everything in place we can train the model quickly and visualize the resulting embedding space. I’ve left out the training details since this is more a post on the statistics side, but its in line with most tutorials out there.

When you train the model you still get a VAE which can produce realistic generations like the ones below, even if we’re using a lossy encoder.

Generations for a VAE with spike and slab prior; latent_dim=10, p=0.8, c^2 = 0.05

What’s different about this model and the normal VAE is that when we encode images we only have a few non-zero components in the embedding representation. If the embedding space is $d$-dimensional we expect the model to activate only $p*d$ dimensions after training, which we can see by looking at the image below:

Each subplot shows the latent representation for a different sample image using the trained model.

There you go! A sparse variational autoencoder which was obtained just from making a few different choices in the statistical scaffolding of the model. I should also note that spike and slab and normal of course aren’t the only choices when designing your VAEs (personal fave of mine is Gumbel Softmax).

---

Quick refresher on VAE’s

In terms of the original VAE proposed (rather offhandedly) by Kingma and Welling in 2014, the story goes something like this: suppose we want to learn the underlying distribution for some data (e.g. images) namely for the purpose of generating samples artificially. Just like in GANs we’d like to be able to convert some samples drawn from a parametric distribution into ones which might have come from our real data generator. This is where the probibalistic decoder, $\theta$, comes into play. The goal of $\theta$ is to map low-dimensional noise into hyperparameters of a parametric distribution which generates realistic high-dimensional samples. Think $x|z \sim f(\theta(z))$

One way to quantify how “good” your decoder is performing is to compute the log probability of a real sample under the decoder framework as

$$\log p_{\theta}(x) = \log \int_{\mathcal{Z}}p_{\theta}(x,z)dz$$

If your decoder is doing its job, then the probability above should be high under your model.

Since this isn’t a really computationally tractable way to go about things however, another way to express the marginal is through importance sampling w.r.t. the posterior distribution over the latents $z$ given a sample $x$ like

$$\log p_{\theta}(x) = \log \int_{\mathcal{Z}}p_{\theta}(x,z) \frac{p_{\theta}(z|x)}{p_{\theta}(z|x)}dz = \log \mathbb{E}_{z\sim p_{\theta}(\cdot | x)}\left[\frac{p_{\theta}(x,z)}{p_{\theta}(z|x)}\right]$$

where we’ve assumed that initially $z\sim p(z)$ (this is the part I’m interested in changing!)

Now this is where the authors got a little sneaky, instead of using the true posterior $p_{\theta}(z|x)$ we can instead come up with a proxy for it through the use of an probibalistic encoder, $\phi$, which turns an input sample into hyperparameters used to model a parametric distribution over the latent space. Think $z|x \sim g(\phi(x))$. With this we write the above as

$$\log p_{\theta}(x) = \log \mathbb{E}_{z\sim q_{\phi}(\cdot | x)}\left[\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}\right]$$

Now by Jensen’s inequality (just geometry!) you arrive at a lower bound on the likelihood of a sample under our variational autoencoder given by the evidence lower bound.

$$\begin{align*} \log \mathbb{E}_{z\sim q_{\phi}(\cdot | x)}\left[\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}\right] &\geq \mathbb{E}_{z\sim q_{\phi}(\cdot | x)}\left[\log \frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}\right]\\ &:= \mathcal{L}(\theta, \phi; x) \end{align*}$$

Therefore maximimzing $\log p_{\theta}(x)$ becomes equivalent to maximizing the ELBO!

Fortunately enough there exists a much nicer representation for the ELBO which is a lot more approachable for us in terms of a numerical optimization perspective; starting (magically) from the KL-divergence between the latent posterior provided by the encoder and the associated prior we get

$$\begin{align*} D_{KL}(q_{\phi}(z|x)||p(z)) &= \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log \frac{q_{\phi}(z|x)}{p(z)}\right]\\ &= \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log \frac{q_{\phi}(z|x)}{p_{\theta}(x,z)p_{\theta}(x|z)^{-1}}\right]\\ &= -\mathcal{L}(\theta, \phi;x) + \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log p_{\theta}(x|z)\right] \end{align*}$$

so that

$$\mathcal{L}(\theta, \phi;x) = \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log p_{\theta}(x|z)\right] - D_{KL}(q_{\phi}(z|x)||p(z))$$

Hmmm I guess this still looks a bit confusing. To make the case for this model a little bit let’s see what happens if we choose to model our probibalistic decoder such that $x|z \sim \mathcal{N}_{n}(\mu_{\theta}(z), 1)$. In this case the first term on the right is proportional to

$$\mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[\log p_{\theta}(x|z)\right] \propto \mathbb{E}_{z\sim q_{\phi}(\cdot|x)}\left[-\frac{1}{2}(x-\mu_{\theta}(z))^{2}\right]$$

So that maximizing this term is equivalent to minimizing the reconstruction loss.

By mixing and matching which probibalisitc frameworks you’re operating with for the encoder prior and posterior, and decoder posterior, the form of the ELBO changes accordingly.

References

• Auto-Encoding Variational Bayes by Kingma et al. (2013)
• beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework by Higgins et al. (2022)